MrBayes by example: Identification of sites under positive selection in a protein

Background:

Professor Walter M. Fitch and assistant research biologist Robin M. Bush of UCI's Department of Ecology and Evolutionary Biology, working with researchers at the Centers for Disease Control and Prevention, studied the evolution of a prevalent form of the influenza A virus during an 11-year period from 1986 to 1997. They discovered that viruses having mutations in certain parts of an important viral surface protein were more likely than other strains to spawn future influenza lineages. Human susceptibility to infection depends on immunity gained during past bouts of influenza; thus, new viral mutations are required for new epidemics to occur. Knowing which currently circulating mutant strains are more likely to have successful offspring potentially may help in vaccine strain selection. The researchers' findings appear in the Dec. 3 issue of Science magazine.

Fitch and his fellow researchers followed the evolutionary pattern of the influenza virus, one that involves a never-ending battle between the virus and its host. The human body fights the invading virus by making antibodies against it. The antibodies recognize the shape of proteins on the viral surface. Previous infections only prepare the body to fight viruses with recognizable shapes. Thus, only those viruses that have undergone mutations that change their shape can cause disease. Over time, new strains of the virus continually emerge, spread and produce offspring lineages that undergo further mutations. This process is called antigenic drift. "The cycle goes on and on-new antibodies, new mutants," Fitch said.

The research into the virus' genetic data focused on the evolution of the hemagglutinin gene-the gene that codes for the major influenza surface protein. Fitch and fellow researchers constructed "family trees" for viral strains from 11 consecutive flu seasons. Each branch on the tree represents a new mutant strain of the virus. They found that the viral strains undergoing the greatest number of amino acid changes in specified positions of the hemagglutinin gene were most closely related to future influenza lineages in nine of the 11 flu seasons tested.

By studying the family trees of various flu strains, Fitch said, researchers can attempt to predict the evolution of an influenza virus and thus potentially aid in the development of more effective influenza vaccines.

The research team is currently expanding its work to include all three groups of circulating influenza viruses, hoping that contrasting their evolutionary strategies may lend more insight into the evolution of influenza.

Along with Fitch and Bush, Catherine A. Bender, Kanta Subbarao and Nancy J. Cox of the Centers for Disease Control and Prevention participated in the study.

Introduction to Bayesian Analyses

Paul Lewis, a colleague of mine at the University of Connecticut is one of the pioneers applying a Bayesian framework to the analysis of molecular data. His lecture notes for his Introduction to Bayesian Phylogenetics are here (about four hours of lecture). Essentially, the Bayesian approach tries to assess the probability of a model, bipartition or range of a parameter value - in contrast to ML, which assesses the probability of the data given a model.

It has been shown that under some conditions the biased sampling of tree and parameter space converges on the posterior probability. The approach most often used in recent months is Markov Chain Monte Carlo sampling. The principle is illustrated by a little program that Paul Lewis wrote called MCRobot. This little robot runs around in two dimensional space over which different distribution can be defined. The walk of the robot is biased in a way so that probability to find the robot in a place is proportional to the defined distribution.

--- MCRobot demo in class ---

MCRobot Exercise. Help file for MCRobot is HERE.

1. Start the program. The black space you look at is the absolutely flat space where robot walks. To start the robot press "Ctrl-F" (you see the 100 steps that robot took connected to each other). To continue walking press "Ctrl-N" [you can hold "Ctrl-N" for the continuous walk]
   
   
2. Run the robot for the sufficient amount of time. How well does the robot explore the space?
   
   
3. Now change the terrain by introducing hills. To do so, drag a mouse somewhere in the space and release the mouse. The hill is depicted as yellow contours. Run the robot for some time. Do you observe any noticeable difference in the robot behavior?
   
   
4. Go to "Chains" menu and toggle "2 chains". Now MCRobot will run two chains simultaneously (cold [original blue] chain, and heated [red chain]). Go to "Show" menu and choose "All chains" to have both chains depicted. Run the chains for some time. Are there any differences in the red and blue chains space exploration?
   
   
5. Go to "Robot"-> "Options", toggle "Allow rotation" option. This will allow the rotation of the plane where the robot walks [before we always looked from the top] To change viewing angle, press right mouse button and rotate the mouse. Now run the chains again. Are there any differences in the red and blue chains space exploration from this angle of view?
   
   

MrBayes is doing the same as the MCRobot, but it walks around in tree and parameter space. For each place it visits, the program calculates the likelihood. The decision to take or reject a step is based on the likelihood. From the evaluation of all the trees and parameters visited (minus the burn-in phase), one can calculate the posterior probabilities of trees and parameters.

Exercise1:

The goal of this exercise is to learn how to use MrBayes to reconstruct phylogenies.

1. Save testseq1c.nex. This is the dataset of vacuolar ATPase A subunit you used earlier, but in the NEXUS format that MrBayes reads. Start MrBayes.

2. At the MrBayes command prompt type "execute testseq1c.nex". This will load the data into the program.

3. Type the following commands one by one:
   
   prset aamodelpr=fixed(jones)
   mcmcp samplefreq=50 printfreq=50 nchains=2 startingtree=random
   mcmcp savebrlens=yes filename=testseq1c
   mcmc ngen=20000
   sump filename=testseq1c
   
   Rather than typing the commands one by one you could use a MrBayes block at the end of the input file:
   begin mrbayes;
       prset aamodelpr=fixed(jones);
       mcmcp samplefreq=50 printfreq=50 nchains=2 startingtree=random;
       mcmcp savebrlens=yes filename=testseq1c;
       mcmc ngen=20000;
       sump filename=testseq1c;
   end;
   
   " prset" sets the priors for the model used to calculate likelihoods. In this case we choose the substitution parameters from the JTT amino acid substitution model (Jones et al., 1992).
   " mcmcp " sets parameters for Markov Chain Monte Carlo: we set to sample every 50 generation, to print results to a screen every 50th generation, run 2 chains simultaneously, start with random tree, save branch lengths an d outfile name will be testseq1c.
   " mcmc " actually runs the chain, and we set it to run for 20000 generations.
   The program runs to analyses in parallel (each with 4 chains). The smaller the reported average standard deviation of split frequencies is, the more reliable the result (i.e., your run is close enough to infinitely long). When the value is below .015, or when your patience is exhausted, terminate the run, by typing no at the prompt.
   
   After the run is finished, the " sump " command will plot the logL vs. generation number, that allows to determine the necessary burnin (you want to discard those samples as "burnin" where the -logL is still rising steadily).
   
4. Type
   " sumt burnin=20 " or " sumt filename=testseq1c burnin=20 "
   , where you need to substitute '20' with the number you obtained in the previous step of the exercise (Note: that burnin values is the # of generations divided by 50, since we sample every 50th generation). This command creates a consensus tree, and shows posterior probabilities of the clades. You can take a look at the tree in Treeview by loading the testseq1.con file. [Rather than using the sump command, you also can import the parameter file into EXEL and plot the logL values as a chart in EXEL. See below.]
   

The goal of this exercise is to detect sites in hemmagglutinin that are under positive selection.

Powerpoint slides on positive selection are here

Since the analysis takes a very long time to run (several days), here are the saved results of the MrBayes run: Fitch_HA.nex.p, Fitch_HA.nex.t.

The original data file is flu_data.paup. The dataset is obtained from an article by Yang et al, 2000. The File used for MrBayes is here


The MrBayes block used to obtain results above is:

begin mrbayes;
set autoclose=yes;
lset nst=2 rates=gamma nucmodel=codon omegavar=Ny98;
mcmcp samplefreq=500 printfreq=500;
mcmc ngen=500000;
sump burnin=50;
sumt burnin=50;
end;

Selecting a nucmodel=codon with Omegavar=Ny98 specifies a model in which for every codon the ratio of the rate of non-synonymous to synonymous substitutions is considered. This ratio is called OMEGA. The Ny98 model considers three different omegas, one equal to 1 (no selection, this site is neutral); the second with omega < 1, these sites are under purifying selection; and the third with Omega >1, i.e. these sites are under positive or diversifying selection. (The problem of this model is that the there are only three distinct omegas estimated, and for each site the probability to fall into one of these three classes. If the omega>1 is estimated to be very large, because one site has a large omega, the other sites might not have a high probability to have the same omega, even though they might also be under positive selection. This leads to the site with largest omega to be identified with confidence, the others have more moderate probabilities to be under positive selection).

1. First, you need to detect how many generations to burn in. Open Fitch_HA.p in Excel and plot # of generations versus -LnL values. Determine after how many generations the graph becomes stationary. The burnin value is that number of generations divided by 50 (since only every 50th generation was sampled; i.e. the burnin value roughly is equal to the number of rows - not quite because there is a header). To more accurately determine the burnin, you need to rescale the Y-axis.
   

(Note: the burnin can also be determined in MrBayes using the sump command:
Start MrBayes. Load the data. To do that, type the following command into MrBayes command prompt:
   execute flu_data.paup;
Now type:
   sump filename=Fitch_HA.nex;
However, usually one needs to adjust the filename ...)

2. Load Fitch_HA.nex.p into Excel. (You need to load the data into 2 sheets, since Excel does not allow to load more than 256 columns per sheet. To load the data, create a new Excel spreadsheet. Go to Data->Get External Data->Import Text File, and load first 256 columns.
If you use a German version of Microsoft, in the import wizard's section on Format, select advanced and then select the correct decimal point symbol, i.e. ".".
Go to a separate sheet, and repeat "Get External Data" command to load the rest of the data, you need to block out (=select =make black) and exclude the first 256 columns). This file contains information for posterior probabilities for each site (columns) at each sampled generation (rows).

3. Calculate average posterior probability for each site of being under positive selection (Do not forget to exclude first N rows as a burnin; you should have detected value of N in the first question of this exercise). (Use AVERAGE() function of Excel)

4. Plot average posterior probability vs. site # . Select a few sites with the highest posterior pro. bability of being positively selected. (Examples are here and here, check all sheets - note: these were calculated from only 30 000 generations)

5. Create a histogram for the omega value <1 and the omega>1. To do this you need to use Analysis ToolPak of Excel (Tools->Data Analyses; if you do not see this item in the Tools menu, you need to activate the ToolPak. To do that go to Tools->Add-Ins... and check "Analysis ToolPak").
The histogram data will be placed into a separate sheet. Again, do not forget to discard the burnin from consideration. Plot the calculated histogram data as a histogram. What is the shape of the distribution?

6. Determine the 95% credibility interval for the omega<1 value. To do this you sort posterior probability column in ascending order (Select data you want to sort, and go to Data->Sort... ). Again, do not forget to discard the burnin; the easiest might be to actually delete it.. After sorting, exclude 2.5% of the data on the top and on the bottom. The range of the remaining data gives you the 95% confidence interval.

7. The structure of hemagglutinin has been crystallized and is publicly available through PDB. Download the PDB file here and examine it with SPDBV. Chain A of the PDB file corresponds to the sequences we did our analysis with (color the molecule according to chain). Below is a comparison of the one of the sequences we used for analyses with the sequence for which the structure was determined:

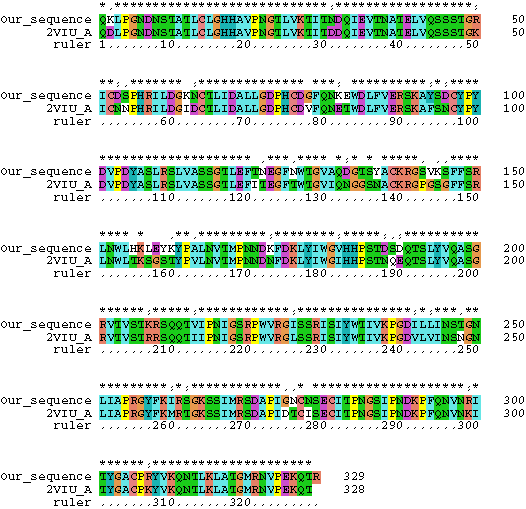
Using this alignment as a help, map the sites which have the highest probability to belong to the class with omega>1. Where are these sites located in the protein? (Reminders: The position number in the nexus file corresponds to nucleotide sequence, the structure is based on the amino acid sequence - take the third codon position and divide by 3 to find the amino acid. You only want to concern with Chain A!)